这道题是第四道题,也是一道非常简单的模板题,随便写写就行了(逃
文章目录
题目描述
这是一道洛谷上的原题,仙人指路:P5318 【深基18.例3】查找文献。
题目描述
小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个(也有可能没有)参考文献的链接指向别的博客文章。小K 求知欲旺盛,如果他看了某篇文章,那么他一定会去看这篇文章的参考文献(如果他之前已经看过这篇参考文献的话就不用再看它了)。
假设洛谷博客里面一共有 \( n \left(n\leq 10^5\right) \) 篇文章(编号为 1 到 n)以及 \( m \left(m\leq 10^6\right) \) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章,请帮助小 K 设计一种方法,使小 K 可以不重复、不遗漏的看完所有他能看到的文章。
这边是已经整理好的参考文献关系图,其中,文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。
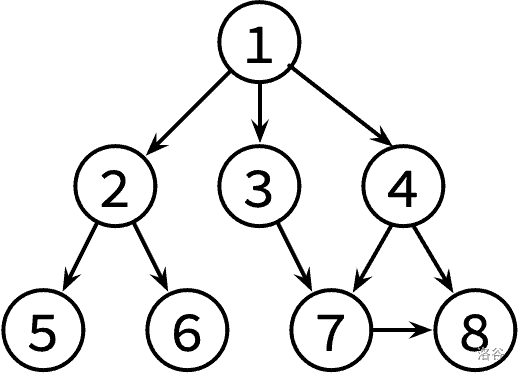
请对这个图分别进行 DFS 和 BFS,并输出遍历结果。如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。
输入格式
无
输出格式
无
输入输出样例
输入 #1
8 9 1 2 1 3 1 4 2 5 2 6 3 7 4 7 4 8 7 8
输出 #1
1 2 5 6 3 7 8 4 1 2 3 4 5 6 7 8
知识链接
图的存储与遍历方法
早就想做一个有关的专题了,正好借此机会写一下。
图的介绍
事实上,我们平常所说的图通常分为两大类:图和网。两者的区别是图中的边没有权值,而网中的边是带有权值的。下文中的图大都代指网。
图的储存方式有很多种:邻接矩阵、邻接表、链式前向星、十字链表、邻接多重表,等等。而平时我们经常用到的只有三种:邻接矩阵、邻接表和链式前向星。其中邻接矩阵是用数组实现;而邻接表和链式前向星则使用链表实现,不过在OI中通常使用数组模拟链表的方式代替链表,这种方式操作更加便捷迅速,且空间上更为紧凑,是通常的实现方式。
邻接矩阵(数组实现)
介绍
邻接矩阵是一种简单却耗空间大的储存方式,空间复杂度为 \( O\left(V^2\right) \)(V为点数,E为边数,下文中也是如此)。下面是邻接矩阵的操作(以无向图为例,下同):
// n是点的个数,编号从0到n-1
// 存储
int graph[n][n];
// graph[i][j]表示从点i到点j有一条权值为graph[i][j]的边
// 初始化
memset(graph, INF, sizeof(graph));
// 存一条边权为w的边 (u, v)
graph[u][v] = w;
graph[v][u] = w; // 注意,无向图中反向边也要存,有向图中删去即可
// 遍历点u的所有邻边
for (int v = u + 1; v < n; ++v) // 注意,无向图中v=u+1,有向图中v=0,请读者自己思考为什么
if (graph[u][v] != INF) // 这里是判断点u和点v之间是否有边相连
... // 可以干你想要的事O(∩_∩)O
优势
- 稠密图下空间利用率高
- 操作简单,代码简短,写起来较为方便
- 对边的存储、查询和更新等操作只需要用很简单的代码就能完成,并且是常数时间
- 可以轻松进行连反边的操作
- 可以很快地删除某条边
不足
- 空间复杂度超标。如上文所述,邻接矩阵的空间复杂度为 \( O\left(V^2\right) \),在稀疏图中,大量的空间会被浪费。事实上,当V=10000时,空间已经超出常见竞赛的空间限制了。事实上,正是空间的原因,使得邻接矩阵成为三种储存方式中垫底的一种
- (基本上)无法储存重边。大家可以从上面邻接矩阵的定义中看出,一个 \( graph\left[i\right]\left[j\right] \) 只能存一个 \( \left(i, j\right) \) 的权值,如果有很多个 \( \left(i, j\right) \) 边,那邻接矩阵只能存储其中一条边。不过这也不是绝对的,详情请参见第2.1.2.4节“邻接矩阵储存重边的特殊情况”
- 遍历成本过高。不论边数为多少,邻接矩阵遍历所有边的复杂度都为 \( O\left(V^2\right) \),就算一个边都没有也还要遍历那么多遍
- 无法处理(或处理起来较为麻烦)点有属性(如有点权等)的情况
【扩展】邻接矩阵储存重边的特殊情况
事实上,“邻接矩阵不能储存重边”不是绝对的。邻接矩阵在存网的时候是不能储存重边的,不过在存图(指无权图)的时候却是可以通过一点小技巧,来使邻接矩阵可以储存重边。由于图中没有边权,所以我们不需要存边权,那么在graph[i][j]中存什么呢?答:边的个数。在这种存图方式中,\( graph\left[i\right]\left[j\right] \) 代表的就是点 \( i \) 和点 \( j \) 之间边的个数。
// 邻接矩阵存图
// 存储,没变
int graph[n][n];
// graph[i][j]表示从点i到点j几条边
// 初始化
memset(graph, 0, sizeof(graph));
// 存一条边 (u, v)
++graph[u][v];
++graph[v][u]; // 注意,无向图中反向边也要存,有向图中删去即可
// 遍历点u的所有邻边
for (int v = u + 1; v < n; ++v) // 注意,无向图中v=u+1,有向图中v=0
for (int i = 0; i < graph[u][v]; ++i) // 如果u和v之间没有边,那么就不会进入循环
... // 处理
如果是网的话,还有没有办法存重边呢?其实是有的,那就是将存储的东西从数字变为链表,如下所示:
// 如此一来,i和j之间所有边的权值都可以存到graph[i][j]中了 list<int> graph[i][j];
看上去很美好,但实际上实用意义极低。一方面,这种方法使得耗费的空间进一步加大,让本就不富裕的邻接矩阵雪上加霜;另一方面,这样做了之后,邻接矩阵的优势(对边的操作快、操作简单)也就大打折扣(或者说不复存在)了,实在是亏本生意啊。一般来说,遇到这种情况,不管是稀疏图还是稠密图,都推荐在下面两种存图方式中选择一种来进行存储,而不是使用这种“改进版”的邻接矩阵。
邻接表(可变长数组模拟)
介绍
邻接表是一种精巧的数据结构,空间复杂度大约为 \( O\left(V + E\right) \)。邻接表有两种实现:一种用在边有属性(如有边权等)的情况下,另一种用在点有属性的情况下。下面我们分别给出代码。
实现一
第一种实现使我们通常使用的邻接表的样子,也是最常用的一种,非常清晰易懂,一些有基础的读者可能已经从代码中看懂了邻接表是什么东西。
// n是点的个数,编号从0到n-1
// 存储
struct Edge { // 边的结构体(有向边)
int to; // to是这条边的终点
int w; // w是这条边的权值
Edge(void);
Edge(int, int);
};
Edge::Edge(void) {
to = w = 0;
}
// 构造函数,方便下面push_back
Edge::Edge(int a, int b) {
to = a;
w = b;
}
vector<Edge> graph[n];
// 初始化
// 邻接表其实不用初始化,不过非得初始化一下的话可以这样
for (int i = 0; i < n; ++i)
graph[i].clear();
// 存一条边权为w的边 (u, v)
graph[u].push_back(Edge(v, w));
graph[v].push_back(Edge(u, w));
// 遍历点u的所有邻边
for (int i = 0; i < graph[u].size(); ++i) {
int v(graph[u][i].to); // 这条邻边的对点是v
... // 处理
}
由上面的代码其实已经可以看出邻接表的结构了。邻接表可以看成一个有 \( V \) 项的数组 \( G \),每一项都是一个链表,与点 \( i \) 相邻的点就加入 \( G_i \) 这个链表中。虽说是链表,但在OI界通常是用vector来代替链表。
实现二
// n是点的个数,编号从0到n-1
// 存储
struct Vertex { // 点的结构体(有权点)
vector<Vertex*> edge;
int w; // 点权
};
Vertex graph[n];
// 初始化
// 不用初始化
// 点u的点权是w_u,点v的点权是w_v
graph[u].w = w_u;
graph[v].w = w_v;
// 存一条边 (u, v)
graph[u].edge.push_back(&graph[v]);
graph[v].edge.push_back(&graph[u]); // 无向图反向存边
// 遍历点u的所有邻边
Vertex v;
for (int i = 0; i < graph[u].edge.size(); ++i) {
v = graph[u].edge[i]; // 这条邻边的对点是v
... // 处理
}
实现二的原理与实现一一样,我就不多赘述了。
优势
- 空间复杂度只有 \( O\left(V + E\right) \),非常节省空间,尤其是稀疏图
- 可以储存重边
- 可以处理有点权的情况
- 可以较快遍历某个点的所有邻居
- 可以很快地删除某个边
不足
- 代码实现较为复杂
- 对边的操作(如查询、更新等)比邻接矩阵更慢一些
- 无法方便地进行连反边等操作
链式前向星(数组模拟)
介绍
链式前向星同样是一种空间复杂度为 \( O\left(V + E\right) \) 的数据结构,但比邻接表所需要的实际空间要小一些。链式前向星的原理与邻接表类似,只不过把一开始的索引剥离成了一个单独的数组,然后将vector替换成了数组模拟的链表。
// n是点的个数,编号从0到n-1;m是边的个数
// 存储
struct Edge { // 边的结构体(有向边)
int to; // to是这条边的终点
int w; // w是这条边的权值
int next; // next是这条边的起点下一个邻边在edge数组中的下标,如果没有下一个边了就为-1
};
int head[n]; // head[u]代表点u的第一条邻边在edge数组中的下标,如果没有邻边则为-1
Edge edge[m << 1]; // 如果是有向图的话就是Edge edge[m];
// 初始化
memset(head, -1, sizeof(head));
// 存一条边权为w的边 (u, v),变量cnt为全局变量,初值为0
// 通常将存边操作写成一个函数
inline void AddEdge(int u, int v, int w) {
edge[cnt].to = v;
edge[cnt].w = w;
edge[cnt].next = head[u];
head[u] = cnt++;
}
AddEdge(u, v, w);
AddEdge(v, u, w); // 无向图反向存边
// 遍历点u的所有邻居,~i是什么操作下面会说
for (int i = head[u]; ~i; i = edge[i].next) {
int v(edge[i].to); // v是点u的邻居
... // 处理
}
链式前向星虽然结构清晰,却很难理解,建议大家多研究几遍上面的代码。如果你有一点链表的基础,你可以很容易地理解上述内容中的难点——遍历点u的所有邻居。从起点开始(i=head[u]),只要没有到达终点(~i),就一直往前走(i=edge[i].next)。其中,~的意思是取反,这个操作有一个特性,那就是当被取反的操作数为-1时,取反结果为0。也就是说,当i=-1时循环就会结束。所以说,这段代码也可以写成这个样子:
for (int i = head[u]; i != -1; i = edge[i].next) {
...
}
优势
- 空间复杂度与邻接表一样,且实际占用空间比邻接表还小
- 可以储存重边
- 可以较快地遍历某个点的邻居
- 可以方便地进行连反边等操作
不足
- 编程复杂度比邻接表稍高
- 无法较容易地处理有点权的情况
- 对边的操作(如查询、更新等)比邻接矩阵更慢一些
- 无法较容易地删除某条边
邻接表 vs. 链式前向星
邻接表和链式前向星都是较为节省空间的高级数据结构,那么我们该如何选择呢?
| 邻接表 | 链式前向星 | |
| 占用空间 | 小 | 更小 |
| 是否可以处理有点权的情况 | 是 | 否 |
| 是否可以连反边 | 困难 | 可以 |
| 是否可以删除边 | 可以 | 困难 |
| 遍历速度 | 非常快 | 快 |
综合来讲,一般情况下我们都会选择使用链式前向星,只有特殊状态下(如需要处理点权、频繁删除边、卡常等情况)才使用邻接表,而邻接矩阵则基本不会使用。
【扩展】边集数组
介绍
先声明一下,这个名字是我瞎起的,如果你从哪本权威的书上看到了和这不一样的名字,请告诉我,我一定改。
边集数组其实从严格意义上不算是图的一种储存方式,它只是把所有的边都存到一个数组里,并没有储存图的关系。边集数组一般用于一些特殊的场景,如对边排序等。
// m是边的个数
// 存储
// 有向边
struct Edge {
int from; // 边的起点
int to; // 边的终点
int w; // 边的权值
};
// 边集数组
Edge edges[m << 1]; // 有向边改为Edge edges[m];
// 添加一条权值为w的边(u, v),cnt为全局变量,初值为0
// 注意:此AddEdge与链式前向星中的不是一个东西!
inline void AddEdge(int u, int v, int w) {
edges[cnt].from = u;
edges[cnt].to = v;
edges[cnt++].w = w;
}
AddEdge(u, v, w);
AddEdge(v, u, w); // 无向图反向储存
优势
- 空间复杂度最低,为 \( O\left(E\right) \)。
- 可以进行一些特殊的操作,比如将所有边按照权值排序等。这一点在某些算法中(如Kruskal)很有用。
不足
- 由于其不具备图的结构,所以说基本上除了上述所说的优势以外基本上没有什么用处了。
图的遍历
图的遍历分为两种:BFS遍历和DFS遍历。下面我将会给出两种遍历方法的代码实现,以无向网为例。
BFS遍历
// n为点数
queue<int> q;
bool is_visited[n];
q.push(0);
memset(is_visited, false, sizeof(is_visited));
// 邻接矩阵
while (!q.empty()) {
int u(q.front());
q.pop();
for (int v = u + 1; v < n; ++v) {
if (graph[u][v] != INF && !is_visited[v]) {
is_visited[v] = true;
q.push(v);
}
}
}
// 邻接表
while (!q.empty()) {
int u(q.front());
q.pop();
for (int i = 0; i < graph[u].size(); ++i) {
int v(graph[u][v].to);
if (!is_visited[v]) {
is_visited[v] = true;
q.push(v);
}
}
}
// 链式前向星
while (!q.empty()) {
int u(q.front());
q.pop();
for (int i = head[u]; ~i; i = edge[i].next) {
int v(edge[i].to);
if (!is_visited[v]) {
is_visited[v] = true;
q.push(v);
}
}
}
DFS遍历
// n为点数
bool is_visited[n];
memset(is_visited, false, sizeof(is_visited));
for (int i = 0; i < n; ++i)
Dfs(i);
// 邻接矩阵
void Dfs(int u) {
if (is_visited[u])
return;
is_visited[u] = true;
for (int v = u + 1; v < n; ++v)
if (graph[u][v] != INF)
Dfs(v);
}
// 邻接表
void Dfs(int u) {
if (is_visited[u])
return;
is_visited[u] = true;
for (int i = 0; i < graph[u].size(); ++i) {
int v(graph[u][i].to);
Dfs(v);
}
}
// 链式前向星
void Dfs(int u) {
if (is_visited[u])
return;
is_visited[u] = true;
for (int i = head[u]; ~i; i = edge[i].next) {
int v(edge[i].to);
Dfs(v);
}
}
解题思路
这题非常简单,所有的内容都在上面的知识链接中,只要在遍历时记录一下路径,边遍历边输出就行了,剩下的细节都在代码中,多看看自然就明白了。
注意:此题必须要使用邻接表存图,因为要对每个点的所有邻居进行排序,而这是链式前向星所做不到的。
代码展示
拒绝抄袭,共创和谐社会[机智]
#include <cstdio> // std::scanf, std::printf, std::putchar
#include <cstring> // std::memset
#include <queue> // std::queue
#include <vector> // std::vector
#include <algorithm> // std::sort
using namespace std;
const int kMaxN(100000);
vector<int> kGraph[kMaxN + 5]; // 邻接表
bool kIsVis[kMaxN + 5]; // 记忆数组,图遍历要用
queue<int> kQueue; // BFS用的队列
void Dfs(int, bool); // DFS遍历
void Bfs(void); // BFS遍历
int main(void) {
int n(0), m(0);
memset(kIsVis, false, sizeof(kIsVis));
scanf("%d %d", &n, &m);
for (int i = 0; i < m; ++i) {
int x(0), y(0);
scanf("%d %d", &x, &y);
kGraph[x].push_back(y); // 邻接表存图
}
// 本题难点之一:排序
for (int i = 1; i < n + 1; ++i)
sort(kGraph[i].begin(), kGraph[i].end());
// DFS遍历
Dfs(1, true);
putchar('\n');
// BFS遍历
Bfs();
putchar('\n');
return 0;
}
void Dfs(int u, bool is_start) {
kIsVis[u] = true;
if (!is_start)
putchar(' ');
printf("%d", u);
for (vector<int>::iterator iter = kGraph[u].begin();
iter != kGraph[u].end(); ++iter)
if (!kIsVis[*iter])
Dfs(*iter, false);
}
void Bfs(void) {
bool is_start(true);
memset(kIsVis, false, sizeof(kIsVis));
kIsVis[1] = true;
kQueue.push(1);
while (!kQueue.empty()) {
int u(kQueue.front());
kQueue.pop();
if (is_start)
is_start = false;
else
putchar(' ');
printf("%d", u);
for (vector<int>::iterator iter = kGraph[u].begin();
iter != kGraph[u].end(); ++iter) {
if (!kIsVis[*iter]) {
kIsVis[*iter] = true;
kQueue.push(*iter);
}
}
}
}
写在最后
这道题是基础中的基础,多看看几遍自己就明白了。若最后代码展示中的代码与知识链接中的有出入,以知识链接中的为准,因为代码展示中的代码是以前写的,可能有点难懂,抱歉哈各位_(:з」∠)_
