洛谷刷题记——T155817 空间站链接

这是第三道题，也是较难的一道题，涉及了较深的图论内容。

文章目录

题目描述

某国已建立n个空间站点，连接任意两点 \( A, B \) 的代价等于 \( \min\{\left\vert x_a – x_b\right\vert ,\left\vert y_a – y_b\right\vert ,\left\vert z_a – z_b\right\vert\} \)。其中 \( \left(x_a, y_a, z_a\right) \) 为点 \( A \) 的空间坐标，\( \left(x_b, y_b, z_b\right) \) 为点 \( B \) 的空间坐标。

请你用最小代价让所有点都相连（直接或间接）。（注意空间站链接距离并不等于两点间直线距离，你可以理解为使用了某种坐标跳跃黑科技）

输入格式

第一行1个正整数n。接下来n行每行3个整数 x，y 和 z表示某个点的空间坐标。（点不会重合）

输出格式

一个整数，表示最小花费。

输入输出样例

输入 #1

输出 #1

说明/提示

【数据规模与约定】

对于 50% 的数据，\( n\leq 4000 \)；
对于 100% 的数据，\( n\leq 100000 \)；坐标在-10亿~10亿间。

知识链接

最小生成树

最小生成树（Minimal Spanning Tree，MST）用于解决一种给你一个无向图，问你如何选取最少的边（或总权值最少的一些边），使得所有点都能直接或间接地相通，即所有点形成一个联通块。那为何称为树呢？我们可以思考一下：把 \( n \) 个点连接起来，用边最少的连接方法是相邻的两个点连一条边，形成一条线，这样子 \( n \) 个点只用 \( \left(n – 1\right) \) 条边。让我们再看一眼树的定义：

在图论中，树（英语：Tree）是一种无向图（undirected graph），其中任意两个顶点间存在唯一一条路径。
引自《树 (图论) – 维基百科》

这不就是我们刚刚找的边嘛！也就是说，现在问题转化成了：在一个无向图中找一棵树，使得树所有边的权值相加最少。

求最小生成树有两种主流算法：Prim算法和Kruskal算法，复杂度分别为 \( O\left(E\log_2V\right) \) 和 \( O\left(E\log_2E\right) \)，其中E为边数，V为点数。

Prim算法

Prim算法基于这样一个简单的贪心思想：优先选择离得最近的点，肯定能得到总边权最小的树。设最小生成树中的点的集合为 \( U \)，最小生成树总边权为 \( S \)，具体做法如下：

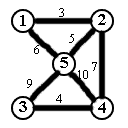
~~（自己手搓的图，太丑了）~~

任选一个起点（假设为1点），将其放入集合中，现在集合 \( U=\{1\} \)。
找到离集合最近的点，是2，加入集合中，现在集合 \( U = \{1, 2\} \)，总边权 \( S = 3 \)。
找到离集合最近的点，是5，加入集合中，现在集合 \( U = \{1, 2, 5\} \)，总边权 \( S = 3 + 5 = 8 \)。
找到离集合最近的点，是1，但1已经在集合中了，丢弃这个点。
找到离集合最近的点，是4，加入集合中，现在集合 \( U = \{1, 2, 5, 4\} \)，总边权 \( S = 8 + 7 = 15 \)。
找到离集合最近的点，是3，加入集合中，现在集合 \( U = \{1, 2, 5, 4, 3\} \)，总边权 \( S = 15 + 4 = 19 \)。
所有的点都在集合中，结束，\( S = 19 \)。

可以看出上面的操作中有两个关键操作：找到离集合最近的点、以及丢弃已有的点。找到离集合最近的点，其实就是找集合中每个点的所有邻居中离这个点最近的点，定义为最近邻居，距离为最近邻居距离，然后对集合中所有点的最近邻居找最近邻居距离最短的一个点，加入集合中。我们可以创建一个集合 \( V \)，每将一个点加入集合 \( U \) 中，就将这个点的所有邻居加入 \( V \) 中，然后将 \( V \) 中距离最近的点加入 \( U \) 中，继续如此操作。我们可以模拟一下：

1被加入 \( U \) 中，\( V = \{\left(2, 3\right), \left(5, 6\right)\} \)。\( \left(2, 3\right) \) 中 \( 2 \) 为点的编号，\( 3 \) 为最近邻居距离。
\( \left(2, 3\right) \) 被取出 \( V \)，加入 \( U \) 中，\( V = \{\left(5, 6\right), \left(4, 7\right), \left(5, 5\right)\} \)。不加 \( \left(1, 3\right) \) 是因为这条边已经被加入最小生成树了。
\( \left(5, 5\right) \) 被取出 \( V \)，加入 \( U \) 中，\( V = \{\left(5, 6\right), \left(4, 7\right), \left(1, 6\right), \left(3, 9\right), \left(4, 10\right)\} \)。
\( \left(1, 6\right) \) 被取出 \( V \)，\( V = \{\left(5, 6\right), \left(4, 7\right), \left(3, 9\right), \left(4, 10\right)\} \)。
\( \left(5, 6\right) \) 被取出 \( V \)，但已被处理过，再取出 \( \left(4, 7\right) \)，加入 \( U \) 中，\( V = \{\left(3, 9\right), \left(4, 10\right), \left(3, 4\right), \left(5, 10\right)\} \)。
\( \left(3, 4\right) \) 被取出 \( V \)，加入 \( U \) 中，\( V = \{\left(3, 9\right), \left(4, 10\right), \left(5, 10\right), \left(5, 9\right)\} \)。
结束

从 \( V \) 中选出最近邻居距离最小的点，可以用for循环遍历一遍，这样做的复杂度是 \( O\left(n\right) \)。但这样做并不太好，我们可以使用一个优先队列，每次插入的复杂度是 \( O\left(\log_2n\right) \)，取出的复杂度是 \( O\left(1\right) \)，总的复杂度是 \( O\left(E\log_2V\right) \)。

由于Prim算法是对点做操作，所以对于稠密图来说Prim算法表现良好。下面给出一份示例代码（链式前向星存图）：

struct Edge {
  int to, next, w;
};

int kHead[kMaxN + 5]; // 链式前向星存图
Edge kEdge[(kMaxM << 1) + 5]; // 同上
bool kIsDone[kMaxN + 5]; // 记录这个点是否已在集合U里
int kDis[kMaxN + 5]; // 记录到某个点的所有边中最短的一条的长度
priority_queue<pair<int, int>, vector<pair<int, int> >,
               greater<pair<int, int> > > kQueue; // 优先队列，集合V

int Prim(void) {
  pair<int, int> u;
  int res(0); // 记录最小生成树的边权和，即S
  memset(kIsDone, 0, sizeof(kIsDone));
  memset(kDis, 0x7f, sizeof(kDis));
  kDis[0]= 0; // 起点的长度设为0
  kQueue.push(make_pair(0, 0)); // 起点入队

  while (!kQueue.empty()) {
    u = kQueue.top(); // 从V中取出距离集合U最近的点
    kQueue.pop();

    if (!kIsDone[u.second]) { // 如果这个点不在集合U里
      kIsDone[u.second] = true; // 把它加入集合U
      res += u.first; // 更新S

      // 遍历这个点的所有邻居
      for (int i = kHead[u.second]; ~i; i = kEdge[i].next) {
        int v(kEdge[i].to);

        if (kEdge[i].w < kDis[v]) { // 如果从这条边到这个点比从其他边到要短
          kDis[v] = kEdge[i].w;
          kQueue.push(make_pair(kEdge[i].w, v)); // 把它的邻居加入集合V
        }
      }
    }
  }

  return res; // 返回边权和
}

Kruskal算法

Kruskal算法也是基于一个简单的贪心思想：每次都选所有边中最短的边，最后加起来肯定是最短的。设最小生成树的边集合为 \( T \)，具体操作如下：

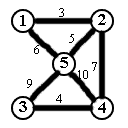
从所有边中选出最小的边，加入 \( T \) 中。最短的边是 \( 1-2 \)，\( T = \{1-2\} \)，边权 \( S = 3 \)。
加入 \( 3-4 \)，\( T = \{1-2, 3-4\} \)，\( S = 3 + 4 = 7 \)。
加入 \( 2-5 \)，\( T = \{1-2, 3-4, 2-5\} \)，\( S = 7 + 5 = 12 \)。
加入 \( 1-5 \)，但发现这样会形成一个圈，丢弃它。
加入 \( 2-4 \)，\( T = \{1-2, 3-4, 2-5, 2-4\} \)，\( S = 12 + 7 = 19 \)。
加入 \( 3-5 \)，但发现这样会形成一个圈，丢弃它。
加入 \( 4-5 \)，但发现这样会形成一个圈，丢弃它。
没有边可以加了，结束，\( S = 19 \)。

上述操作中有一个关键操作：判断是否形成了一个圈。我们判断加上这个边后是否会形成圈，只要判断这个边的两个端点是否联通即可。如果这条边的两个端点联通，那么加上这条边后肯定会形成一个圈，读者可以思考一下为什么。至于判断两个端点是否联通，我们可以使用并查集。每加入一条边，就把这条边的两个端点加入到一个并查集中，代表这两个点是联通的。对边排序的复杂度是 \( O\left(E\log_2E\right) \)，加边的复杂度是 \( O\left(E\right) \)，总复杂度是 \( O\left(E\log_2E + E\right) \approx O\left(E\log_2E\right) \)。其实还可以再做一点小优化：由最小生成树的定义可知，其实加了 \( \left(n – 1\right) \) 条边后就已经完成了最小生成树的构造，正如上面例子中的第5步时就可以结束了，后面的第7，8步都是浪费的，也就是说当加的边数到达 \( \left(n – 1\right) \) 时就可以直接结束算法。

Kruskal算法在稀疏图中速度更快，并且由于良好的复杂度和简单的编码，使得Kruskal算法比Prim算法应用更广。下面给出一份示例代码（边集数组存图）：

struct Edge {
  int from, to, w;
};

Edge kEdges[(kMaxM << 1) + 5]; // 边集数组，和Kruskal算法极为匹配

// 自定义比较函数
bool Cmp(const Edge& x, const Edge& y) {
  return x.w < y.w;
}

int Kruskal(int n, int m) {
  int added_edge(0), res(0); // added_edge记录已经添加的边的数量
  sort(kEdges, kEdges + m, Cmp);

  for (int i = 0; i < m && added_edge != n - 1; ++i) {
    if (UnionSet(kEdges[i].from, kEdges[i].to)) { // 并查集操作，如果两个点联通（即在同一个集里，有同一个“大哥”），返回false并合并两点，否则返回true
      res += kEdges[i].w; // 加边
      ++added_edge;
    }
  }

  return res;
}

通常情况下，我们都是使用Kruskal算法。

解题思路

当我第一眼看到这题的时候，我直接懵了：现在普及组都考解析几何了吗？当我第二眼看过去的时候，才发现这其实是一道最小生成树的裸题。本题的解答步骤可以分为三部分：问题建模（即将问题转化为求最小生成树）、48pts方法和AC方法。

问题建模

本题中的三维坐标啊、求距离啊、空间跳跃啊什么的，看上去很唬人，实际上只要仔细分析可知，这个三维坐标的用处其实就是用来求两点间距离的，没别的用处。我们可以将其转化为普通的图论题：给每个点编一个号，从0~n-1（从1~n也行），这就将空间中的这些“三维点”转化为了一些简单的一维点。当然，这还远远不够，因为我们要将其转化为可以用最小生成树求解的问题。我们可以分析一下，我们要在本没有路的地方修路，不就是在全部都是路的地方选路走嘛！我们把所有的点都连起来，也就是说每个点都与其他点直接相连，一共要连 \( \frac{n\left(n – 1\right)}{2} \) 条边，每条边的长度就是两点之间的距离，这就做到了“全都是路”这一点，这就形成了一个普通的图，可以直接用最小生成树求解。

48pts方法

经过了上面的问题建模后，我们可以直接使用最小生成树求解。由于这是一个不折不扣的稠密图（废话，稠得不能再稠了），所以我们直接使用邻接矩阵存图＋Prim算法求解。

但是，当我们想要动手做的时候，却突然发现~~恶意满满的~~数据范围：\( n\leq 100000 \)。这如果真的要把图存下来，由于空间复杂度是 \( O\left(n^2\right) \)，那这数组真的是炸开花得不能再炸开花了。怎么办呢？我们仔细分析一下Prim算法的过程中有哪些操作用到了图：一、遍历这个点所有的邻居；二、获取这个点到它邻居的距离。细心的你看到这里可能已经发现了：在咱们的图里，某个点的邻居不就是其他所有的点嘛！至于距离，可以直接用两点的公式算出来，根本不需要存图。这样下来，我们只需要一个存点的数组，放在这题目下绰绰有余了。

这时候，我们来算一下，时间复杂度：点有 \( n \) 个，而边则有 \( \frac{n\left(n – 1\right)}{2} \approx n^2 \) 条，则运算次数大约为 \( O\left(E\log_2V\right)\approx 1.66\times 10^{11} \) 次，要说一秒算完着实是有些勉强。所以说这个算法只能拿到一半的分，要全部AC还得用更好的算法。下面给出48pts的代码：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cctype>

#include <queue>
#include <utility>
#include <functional>
#include <vector>
#include <limits>

using namespace std;

const int kMaxN(100000);
const int kBufSize(100000);

// 点
struct Point {
  int x, y, z;

  Point(void);
  Point(int, int, int);
};

char kBuff[kBufSize + 5]; // 快读用
Point* kPoints[kMaxN + 5]; // 点集数组
long long kDis[kMaxN + 5]; // 见上面Prim代码
bool kIsDone[kMaxN + 5];
priority_queue<pair<long long, int>, vector<pair<long long, int> >,
               greater<pair<long long, int> > > kQueue;

inline int Read(char**, char**); // 快读
inline char ReadChar(char**, char**); // 快读
long long Prim(int);
inline long long PointDis(int, int); // 求两点间距离
inline long long MyMin(long long, long long, long long); // 求三数中最小的数

int main(void) {
  const long long kMaxLL(numeric_limits<long long>::max() - 1);
  memset(kBuff, '\0', sizeof(kBuff)); // 快读用
  char* head(kBuff), *tail(kBuff); // 快读用
  int n(Read(&head, &tail));
  memset(kDis, 0, sizeof(kDis));
  memset(kIsDone, false, sizeof(kIsDone));

  for (int i = 0; i < n; ++i)
    kPoints[i] = new Point(Read(&head, &tail), Read(&head, &tail),
                           Read(&head, &tail)); // 读点

  for (int i = 0; i < n; ++i)
    kDis[i] = kMaxLL; // 将距离初始化为最大值，memset没法初始化long long

  printf("%lld\n", Prim(n)); // 输出最小生成树

  for (int i = 0; i < n; ++i)
    delete kPoints[i];

  return 0;
}

Point::Point(void) {
  x = y = z = 0;
}

Point::Point(int a, int b, int c) {
  x = a;
  y = b;
  z = c;
}

inline int Read(char** head, char** tail) {
  bool flag(true);
  char ch(ReadChar(head, tail));
  int num(0);

  while (!isdigit(ch)) {
    if ('-' == ch)
      flag = false;
    ch = ReadChar(head, tail);
  }

  while (isdigit(ch)) {
    num = (num << 3) + (num << 1) + (ch ^ 48);
    ch = ReadChar(head, tail);
  }

  return flag ? num : ~(num - 1);
}

inline char ReadChar(char** head, char** tail) {
  if (*head == *tail) {
    *head = kBuff;
    *tail = kBuff + fread(kBuff, 1, kBufSize, stdin);
  }

  return *head == *tail ? EOF : *(*head)++;
}

// Prim算法模板
long long Prim(int n) {
  pair<long long, int> u;
  long long res(0);
  kDis[0] = 0;
  kQueue.push(make_pair(0, 0));

  while (!kQueue.empty()) {
    u = kQueue.top();
    kQueue.pop();

    if (!kIsDone[u.second]) {
      kIsDone[u.second] = true;
      res += u.first;

      // 遍历所有邻居，即除自己外所有的点
      for (int i = 0; i < n; ++i) {
        long long dis(PointDis(u.second, i)); // 算出两点间距离

        if (dis < kDis[i]) {
          kDis[i] = dis;
          kQueue.push(make_pair(dis, i));
        }
      }
    }
  }

  return res;
}

// 求两点间距离
inline long long PointDis(int x, int y) {
  return MyMin(abs(static_cast<long long>(kPoints[x]->x) - kPoints[y]->x),
               abs(static_cast<long long>(kPoints[x]->y) - kPoints[y]->y),
               abs(static_cast<long long>(kPoints[x]->z) - kPoints[y]->z));
}

// 求三数中最小的数
inline long long MyMin(long long a, long long b, long long c) {
  long long min_num(0);

  if (a > b)
    min_num = b;
  else
    min_num = a;

  return c < min_num ? c : min_num;
}

代码很简单，有近三分之一代码长度花在快读上了~~（试图卡常）~~，可惜只能拿一半的分。

AC方法

经过仔细思考后我们可以看出，上述算法中有很多无用的计算，那么我们能不能做出优化呢？三维的有点难搞，我们将其转化为二维进行。

观察下面坐标系中的点：

现在我们将它们互相之间连起来线，找出其中的最小生成树（红线部分）。

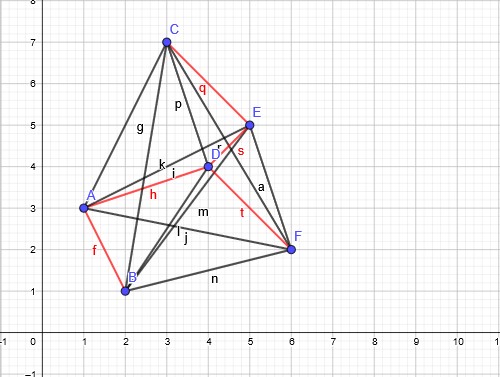
题外话：找最小生成树时我耗费了二十分钟时间把每条边的长度都算出来了，结果上颜色的时候发现GeoGebra自带就有线段长度[奔溃ing]

现在我们改变连接线段的方式，每个点只与离它x轴上最近的点和y轴上最近的点相连，然后再在上面标出最小生成树。

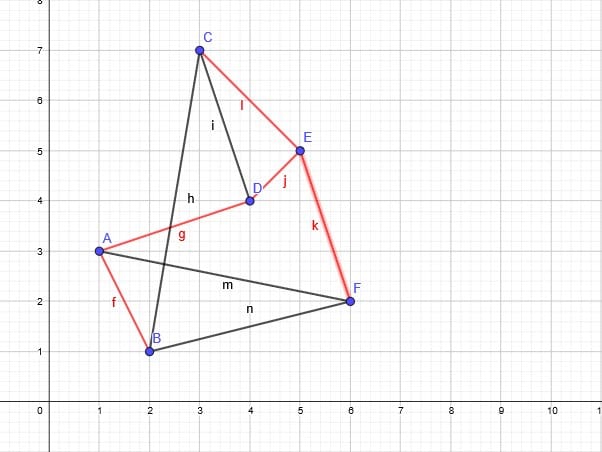
通过仔细观察，我们可以发现，在这个简化版的图中的最小生成树与之前那个完全图中的最小生成树一模一样！

现在，我提出一条猜想：在任何一种我能想象得到的情况中，完全图和简化图的最小生成树都是一模一样的。严谨的证明我也不会，但是本着大胆猜测、不用求证的思想，我们可以简单地用贪心思想解释一下：求最小生成树的过程本质上就是找最短的路，而从一个点到达另一个点，简化图中的路径显然不会比完全图中的长，吧啦吧啦吧啦······（瞎掰）

现在，我们已经证明了这条猜想······（啪）好吧，不过我们能够直观地理解它是对的。这条猜想至关重要，因为它可以将边的数量从 \( \frac{n\left(n – 1\right)}{2} \) 减少到 \( 2\left(n – 1\right) \)，这意味着什么呢？意味着我们成功地AC了！按照之前的计算方法来看，是可以轻松过的。由于边数在 \( O\left(n\right) \) 这个级别，我们可以直接使用边集数组存图＋Kruskal求解最小生成树的方式解决这道题······

等一下，刚才我们是在二维的平面下推出的猜想，那在这个三维的空间中是否适用呢？答案是适用的，至于为什么，请读者自己证明······（啪）。这样子我们就可以将点先按x轴排序，连边，再按y轴排序，连边，最后再按z轴排序，连边，就把图造出来了。

代码展示

拒绝抄袭，共创和谐社会[机智]

#include <cstdio> // std::fread, std::printf
#include <cstring> // std::memset
#include <cctype> // std::isdigit
#include <cstdlib> // std::abs

#include <algorithm> // std::sort

using namespace std;

const int kMaxN(100000);
const int kBufSize(100000);

// 点
struct Point {
  int num, x, y, z;

  Point(void);
  Point(int, int, int, int);
};

// 边
struct Edge {
  int from, to, w;
};

char kBuff[kBufSize + 5]; // 快读，忽视即可
Point* kPoints[kMaxN + 5]; // 点集
Edge* kEdges[(kMaxN << 2) + kMaxN + 5]; // 边集
int kUfs[kMaxN + 5]; // 并查集
int kHeight[kMaxN + 5]; // 并查集高度辅助数组

inline int Read(char**, char**); // 快读，下同
inline char ReadChar(char**, char**);
bool CmpX(Point*, Point*); // 将点按X轴排序
inline void AddEdge(int, int*); // 加边
int PointDis(int, int); // 算两点间距离
inline int MyMin(int, int, int); // 求三数中最小数
bool CmpY(Point*, Point*); // 按Y轴排序
bool CmpZ(Point*, Point*); // 按Z轴排序
long long Kruskal(int, int); // Kruskal主体函数
bool CmpEdge(Edge*, Edge*); // 对边排序
bool UnionSet(int, int); // 并查集，下同
int FindSet(int);
inline void DeleteEdge(int); // 删边，没啥用

int main(void) {
  memset(kBuff, '\0', sizeof(kBuff));
  char* head(kBuff), *tail(kBuff);
  int n(Read(&head, &tail)), edge_cnt(0);
  memset(kUfs, 0, sizeof(kUfs));
  memset(kHeight, 0, sizeof(kHeight));

  for (int i = 0; i < n; ++i)
    kUfs[i] = i;

  for (int i = 0; i < n; ++i)
    kPoints[i] = new Point(i, Read(&head, &tail), Read(&head, &tail),
                           Read(&head, &tail));

  // 排序，分别加边
  sort(kPoints, kPoints + n, CmpX);
  AddEdge(n, &edge_cnt);
  sort(kPoints, kPoints + n, CmpY);
  AddEdge(n, &edge_cnt);
  sort(kPoints, kPoints + n, CmpZ);
  AddEdge(n, &edge_cnt);

  printf("%lld\n", Kruskal((n << 1) + n, edge_cnt)); // 直接Kruskal即可

  // 下面可忽略
  for (int i = 0; i < n; ++i)
    delete kPoints[i];

  DeleteEdge(edge_cnt);

  return 0;
}

Point::Point(void) {
  num = x = y = z = 0;
}

Point::Point(int a, int b, int c, int d) {
  num = a;
  x = b;
  y = c;
  z = d;
}

inline int Read(char** head, char** tail) {
  bool flag(true);
  char ch(ReadChar(head, tail));
  int num(0);

  while (!isdigit(ch)) {
    if ('-' == ch)
      flag = false;
    ch = ReadChar(head, tail);
  }

  while (isdigit(ch)) {
    num = (num << 3) + (num << 1) + (ch ^ 48);
    ch = ReadChar(head, tail);
  }

  return flag ? num : ~(num - 1);
}

inline char ReadChar(char** head, char** tail) {
  if (*head == *tail) {
    *head = kBuff;
    *tail = kBuff + fread(kBuff, 1, kBufSize, stdin);
  }

  return *head == *tail ? EOF : *(*head)++;
}

bool CmpX(Point* x, Point* y) {
  if (x->x == y->x)
    return x->num < y->num;
  else
    return x->x < y->x;
}

bool CmpY(Point* x, Point* y) {
  if (x->y == y->y)
    return x->num < y->num;
  else
    return x->y < y->y;
}

bool CmpZ(Point* x, Point* y) {
  if (x->z == y->z)
    return x->num < y->num;
  else
    return x->z < y->z;
}

bool CmpEdge(Edge* x, Edge* y) {
  return x->w < y->w;
}

inline void AddEdge(int n, int* cnt) {
  //将所有相邻的点相连
  for (int i = 0; i < n - 1; ++i) {
    kEdges[*cnt] = new Edge;
    kEdges[*cnt]->from = kPoints[i]->num;
    kEdges[*cnt]->to = kPoints[i + 1]->num;
    kEdges[(*cnt)++]->w = PointDis(i, i + 1);
  }
}

// 求出距离
int PointDis(int x, int y) {
  return MyMin(abs(kPoints[x]->x - kPoints[y]->x),
               abs(kPoints[x]->y - kPoints[y]->y),
               abs(kPoints[x]->z - kPoints[y]->z));
}

inline int MyMin(int a, int b, int c) {
  int min_num(a > b ? b : a);
  return c < min_num ? c : min_num;
}

inline void DeleteEdge(int edge_num) {
  for (int i = 0; i < edge_num; ++i)
    delete kEdges[i];
}

// Kruskal模板
long long Kruskal(int n, int edge_num) {
  int added_edge(0);
  long long res(0);
  sort(kEdges, kEdges + edge_num, CmpEdge);

  for (int i = 0; i < edge_num && added_edge != n - 1; ++i) {
    if (UnionSet(kEdges[i]->from, kEdges[i]->to)) {
      res += kEdges[i]->w;
      ++added_edge;
    }
  }

  return res;
}

// 并查集模板
bool UnionSet(int x, int y) {
  int a(FindSet(x)), b(FindSet(y));

  if (a == b)
    return false;

  if (kHeight[a] == kHeight[b]) {
    ++kHeight[a];
    kUfs[b] = a;
  } else {
    if (kHeight[a] < kHeight[b])
      kUfs[a] = b;
    else
      kUfs[b] = a;
  }

  return true;
}

int FindSet(int x) {
  int root(x);

  while (kUfs[root] != root)
    root = kUfs[root];

  int tmp1(x), tmp2(0);

  while (tmp1 != root) {
    tmp2 = kUfs[tmp1];
    kUfs[tmp1] = root;
    tmp1 = tmp2;
  }

  return root;
}

写在最后

这道题其实算法方面很容易想到是最小生成树，但这道题主要考察思维能力，如果没想到简化图的方法就只能拿到48pts，非常之可惜。希望我以后也能思维灵活一些。加油↖(^ω^)↗

题目描述

题目描述

输入格式

输出格式

输入输出样例

输入 #1

输出 #1

说明/提示

知识链接

最小生成树

Prim算法

Kruskal算法

解题思路

问题建模

48pts方法

AC方法

代码展示

写在最后

Related posts:

发表评论 取消回复

发表评论取消回复